Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
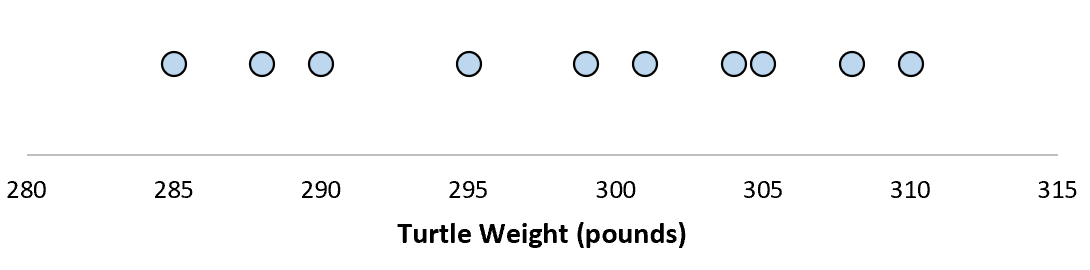
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
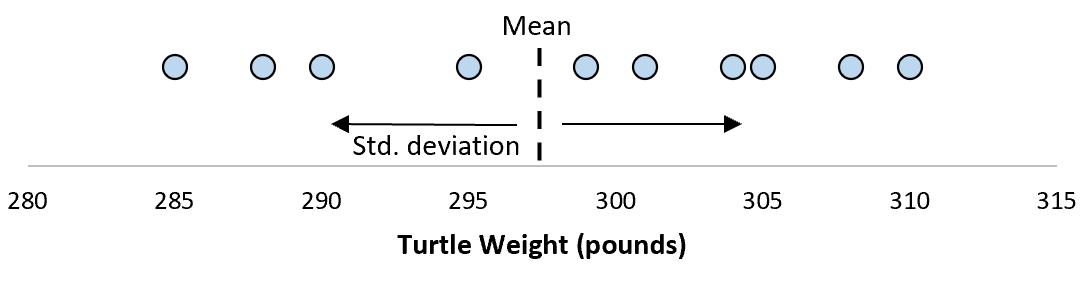
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
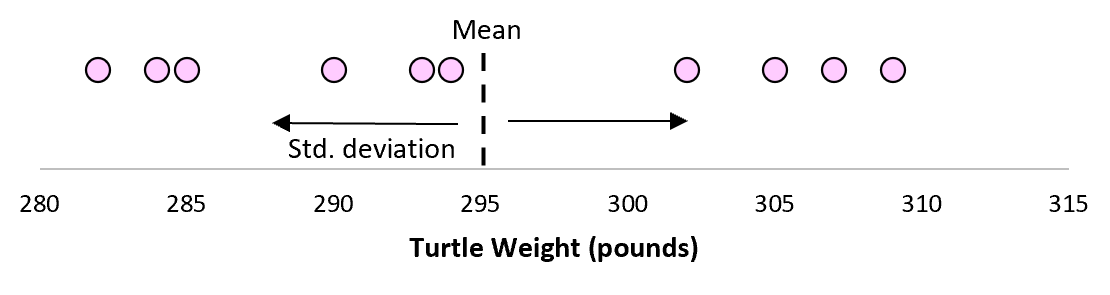
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
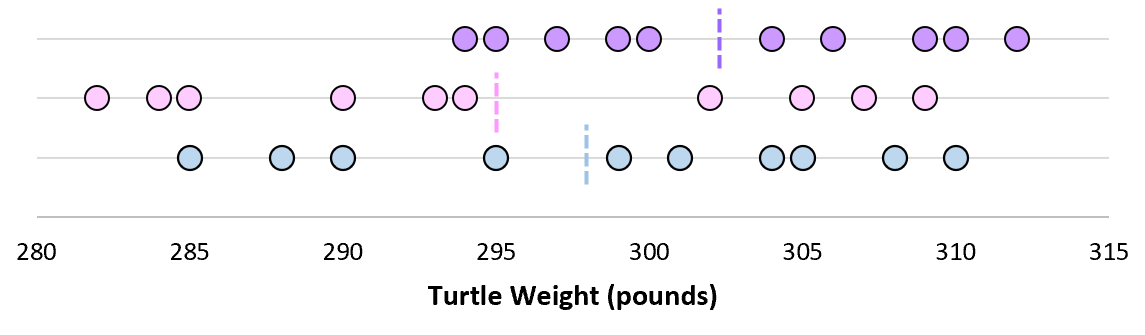
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
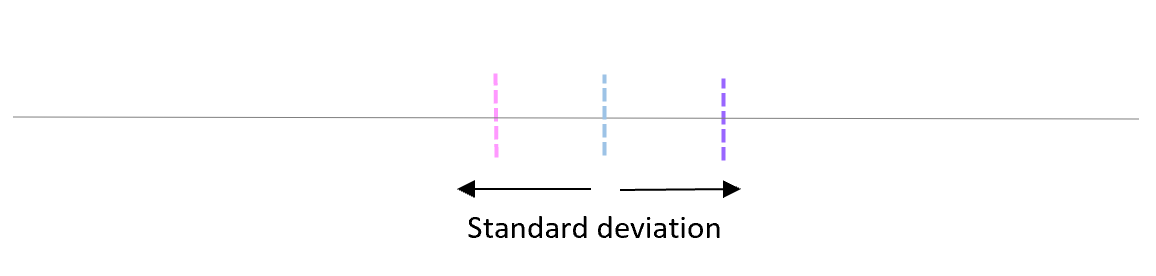
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
The standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Основные выводы:
-
Стандартная ошибка среднего указывает, насколько среднее значение генеральной совокупности может отличаться от среднего выборочного.
-
Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
-
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для обобщения наборов данных.
Если вы собираете данные для научных или статистических целей, стандартная ошибка среднего может помочь вам определить, насколько точно набор данных представляет фактическую совокупность. Проверка точности вашего образца подтверждает ваше клиническое исследование и помогает вам сделать правильные выводы.
В этой статье мы определяем стандартную ошибку среднего, объясняем, как она отличается от стандартного отклонения, и предлагаем формулу для ее расчета.
Какова стандартная ошибка среднего?
Стандартная ошибка среднего (SEM) используется для определения различий между более чем одной выборкой данных. Это помогает вам оценить, насколько хорошо ваши выборочные данные представляют всю совокупность, измеряя точность, с которой выборочные данные представляют совокупность, используя стандартное отклонение.
В статистике, среднеквадратичное отклонение является мерой того, насколько разбросаны числа. Иметь в виду относится к среднему числу. Стандартные функции ошибок используются для проверки точности выборки из нескольких выборок путем анализа отклонений в пределах средних значений.
Высокая стандартная ошибка показывает, что средние значения выборки широко разбросаны по среднему значению генеральной совокупности, поэтому ваша выборка может не точно представлять вашу генеральную совокупность. Низкая стандартная ошибка показывает, что средние значения выборки близко распределены вокруг среднего значения совокупности, что означает, что ваша выборка репрезентативна для вашей совокупности. Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
Например, если вы измерите вес большой выборки мужчин, их вес может варьироваться от 125 до более чем 300 фунтов. Однако, если вы посмотрите на среднее значение выборочных данных, образцы будут различаться всего на несколько фунтов. Затем вы можете использовать стандартную ошибку среднего, чтобы определить, насколько вес отличается от среднего.
Связанный: Как рассчитать стандартную ошибку в Excel (с советами)
Стандартная ошибка среднего по сравнению со стандартным отклонением
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для суммирования наборов данных.
Стандартная ошибка среднего значенияСтандартное отклонениеОценивает изменчивость в нескольких выборках генеральной совокупностиОписывает изменчивость в пределах одной выборкиВыводная статистика, которую можно оценитьОписательная статистика, которую можно рассчитатьИзмеряет, насколько вероятно, что среднее значение выборки будет отличаться от фактического среднего значения в популяции. выборка отличается от фактического среднего значенияСтандартная ошибка — это стандартное отклонение, деленное на квадратный корень размера выборкиСтандартное отклонение — это квадратный корень из дисперсии
Стандартная ошибка средней формулы
Формула для стандартной ошибки среднего выражается как:
SE = σ/√n
-
SE = стандартная ошибка выборки
-
σ = стандартное отклонение выборки
-
n = размер выборки
Обратите внимание, что σ — это греческая буква сигма, а √ — символ квадратного корня.
Формула стандартного отклонения выборки выражается следующим образом:
-
x̄ = среднее значение выборки, сначала найдите это значение
-
xᵢ = отдельные значения x
-
x = значение в наборе данных
-
n = количество точек данных
-
Σ — это сигма-обозначение для суммирования
Вот шаги, которые вы можете использовать для расчета стандартной ошибки среднего, используя выборку из пяти результатов теста SAT. Сначала рассчитайте стандартное отклонение, а затем подставьте это значение в формулу SEM.
1. Рассчитайте среднее
Сложите все образцы вместе и разделите общую сумму на количество образцов.
Пример: пять общих баллов SAT: 1000 + 1200 + 820 + 1300 + 680 = 5000.
Среднее (мк) = 5000 / 5 = 1000
2. Рассчитать отклонение от среднего
Рассчитайте отклонение каждого измерения от среднего, вычитая отдельные измерения из среднего.
Пример. Вычтите средний балл SAT, равный 1000, из каждого балла SAT.
хᵢ — мю
1000 — 1000 = 0
1200 — 1000 = 200
820 — 1000 = -180
1300 — 1000 = 300
680 — 1000 = -320
3. Возведите в квадрат каждое отклонение от среднего
Вычислите квадрат отклонения каждого измерения от среднего. Измерения, которые были отрицательными, после возведения в квадрат станут положительными.
Пример: Найдите квадратный корень отклонения каждой оценки от среднего.
(xᵢ — μ)²
0² = 0
200² = 40000
-180² = 32400
300² = 90000
-320² = 102400
4. Рассчитайте сумму квадратов отклонений
Определить сумму квадратов отклонений, сложив все числа из третьего шага.
Пример: 0 + 10 + 40000 + 32400 + 90000 + 102400 = 264810 = Σ
5. Разделите эту сумму на количество точек данных.
Возьмите сумму, которую вы подсчитали на четвертом шаге, и разделите ее на единицу меньше размера выборки. Используя приведенную выше формулу, это будет выглядеть как n-1.
Пример: 264810 / (5-1) = 66202,5
6. Вычислить квадратный корень, чтобы найти стандартное отклонение
Возьмите квадратный корень из числа, которое вы вычислили на пятом шаге. Это даст вам стандартное отклонение.
Пример: σ = √ 66202,5 = 257,298
7. Разделите стандартное отклонение на квадратный корень из размера выборки.
Используя стандартное отклонение, которое вы определили на шестом шаге, разделите это число на квадратный корень из размера выборки. Это позволит вам определить стандартную ошибку.
Пример: SE = σ/√n
SE = 257,298/√5
SE = 115,067
8. Рассчитайте стандартную ошибку среднего
Вычтите из среднего значения стандартную ошибку и запишите это число. Это стандартная ошибка ниже среднего. Затем добавьте стандартную ошибку к среднему значению и запишите число. Это стандартная ошибка выше среднего.
Пример:
SE ниже среднего: 1000 — 115,067 = 884,933
SE выше среднего: 1000 + 115,067 = 1115,067
Стандартная ошибка среднего может быть представлена следующим образом:
Средний балл SAT случайной выборки испытуемых составляет 1000 ± 115,067.
Пример СЭМ
Чтобы понять силу информации, которую вы можете получить из случайной выборки, используя стандартную ошибку среднего, рассмотрим следующий пример.
Вам дан вес при рождении 17 000 детей, рожденных в больницах Нью-Йорка. Средний вес при рождении составлял семь фунтов и три унции, а стандартное отклонение — один фунт три унции. Допустим, вы хотели узнать средний вес при рождении в этом районе, но получили веса только 30 случайных рождений по сравнению с общей численностью населения. Если бы эта выборка была взята только из всего населения, то вам лучше всего было бы предположить, что средний вес при рождении в выборке также будет равен семи фунтам и трем унциям.
Это предположение вряд ли будет точным, поскольку среднее значение выборки из 30 не будет таким точным, как среднее значение выборки из 17 000. Если бы вы продолжали брать случайные выборки из 30, вполне вероятно, что среднее значение каждой из них несколько изменилось бы.
Поскольку стандартное отклонение генеральной совокупности обычно неизвестно, вам необходимо оценить его, используя стандартное отклонение выборки. Чтобы сделать это с некоторой точностью, ваша выборка должна иметь нормальное распределение и состоять как минимум из 20 измерений. Хотя оценка может быть не совсем точной даже при большой выборке, ошибки в выборочной оценке стандартного отклонения генеральной совокупности будут уменьшены, если вы разделите его на квадратный корень из размера выборки.
Допустим, у вас есть шесть случайных выборок из 30 масс при рождении со стандартными отклонениями 1,3 фунта, 1,16 фунта, 1,14 фунта, 1,2 фунта, 1,25 фунта и 1,19 фунта, что на 0,098 фунта отличается от истинного значения стандартного отклонения населения. Эти шесть образцов приводят к оценкам стандартной ошибки, которые находятся в пределах 0,017 фунта от истинного значения. Ошибки стандартной ошибки средних оценок меньше, чем ошибки оценок стандартного отклонения, а значит, они более точные. Если бы размер выборки был больше 30, стандартная ошибка среднего была бы еще больше уменьшена.
Что такое Стандартная формула ошибки?
Стандартная ошибка — это ошибка, которая возникает в распределении выборки при выполнении статистического анализа. Это вариант стандартного отклонения, так как оба понятия соответствуют мерам спреда. Высокая стандартная ошибка соответствует более высокому разбросу данных для взятой выборки. Вычисление формулы стандартной ошибки выполняется для выборки. В то же время стандартное отклонение определяет генеральную совокупность.
Оглавление
- Что такое Стандартная формула ошибки?
- Объяснение
- Пример формулы стандартной ошибки
- Калькулятор стандартной ошибки
- Актуальность и использование
- Стандартная формула ошибки в Excel
- Рекомендуемые статьи
Следовательно, стандартная ошибка среднего значения будет выражаться и определяться в соответствии с соотношением, описанным следующим образом:
σ͞x = σ/√n
Здесь,
- Стандартная ошибка, выраженная как σ͞x.
- Стандартное отклонение совокупности выражается как σ.
- Количество переменных в выборке, выраженное как n.
В статистическом анализе среднее значение, медиана и мода являются центральной тенденцией. Центральная тенденция Центральная тенденция — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее с помощью 3 различных мер, т. е. среднего, медианы и моды.Подробнее меры. Стандартное отклонение, дисперсия и стандартная ошибка среднего классифицируются как меры изменчивости. Стандартная ошибка среднего для выборочных данных напрямую связана со стандартным отклонением большей совокупности и обратно пропорциональна или связана с квадратным корнем. число. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Более того, эта функция принимает один аргумент из нескольких переменных, используемых для создания выборки. Следовательно, если размер выборки Размер выборкиФормула размера выборки отображает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера генеральной совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности. Если больше, то может быть равная вероятность того, что стандартная ошибка также будет большой.
Объяснение
Можно объяснить формулу для стандартной ошибки среднего, используя следующие шаги:
- Определите и организуйте выборку и определите количество переменных.
- Затем среднее значение выборки соответствует количеству переменных, присутствующих в выборке.
- Затем определите стандартное отклонение выборки.
- Затем определите квадратный корень из числа переменных, включенных в выборку.
- Теперь разделите стандартное отклонение, вычисленное на шаге 3, на полученное значение на шаге 4, чтобы получить стандартную ошибку.
Пример формулы стандартной ошибки
Ниже приведены примеры формул для расчета стандартной ошибки.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон стандартной формулы ошибки Excel здесь — Стандартная формула ошибки Шаблон Excel
Пример №1
Возьмем в качестве примера акции ABC. В течение 30 лет акции приносили средний долларовый доход в размере 45 долларов. Кроме того, было замечено, что акции приносят прибыль со стандартным отклонением в 2 доллара. Помогите инвестору рассчитать общую стандартную ошибку средней доходности, предлагаемой акцией ABC.
Решение:
- Стандартное отклонение (σ) = $2
- Количество лет (n) = 30
- Средняя доходность в долларах = 45 долларов.
Расчет стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 2 доллара США/√30
- = 2 доллара США / 5,4773
Стандартная ошибка,
- σx = 0,3651 доллара США
Таким образом, инвестиция предлагает инвестору стандартную долларовую ошибку в среднем 0,36515 доллара при удерживании позиции ABC в течение 30 лет. Однако, если бы акции сохранялись для более высокого инвестиционного горизонта, то стандартная ошибка среднего значения в долларах значительно уменьшилась бы.
Пример #2
Возьмем в качестве примера инвестора, который получил следующую доходность акций XYZ:
Год инвестиций Предлагаемая доходность120%225%35%410%
Помогите инвестору рассчитать общую стандартную ошибку средней доходности акций XYZ.
Решение:
Сначала определите среднее значение доходности, как показано ниже: –
- ͞X = (x1+x2+x3+x4)/количество лет
- = (20+25+5+10)/4
- =15%
Теперь определите стандартное отклонение доходности, как показано ниже: –
- σ = √ ((x1-͞X)2 + (x2-͞X)2 + (x3-͞X)2 + (x4-͞X)2) / √ (количество лет -1)
- = √ ((20-15) 2 + (25-15) 2 + (5-15) 2 + (10-15) 2) / √ (4-1)
- = (√ (5) 2 + (10) 2 + (-10) 2 + (-5) 2 ) / √ (3)
- = (√25+100+100+25)/ √ (3)
- =√250/√3
- =√83,3333
- «=» 9,1287%
Теперь вычисление стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 9,128709/√4
- = 9,128709/2
Стандартная ошибка,
- σx = 4,56%
Таким образом, инвестиции предлагают инвестору стандартную ошибку в долларах в среднем 4,56% при удержании позиции XYZ в течение 4 лет.
Калькулятор стандартной ошибки
Вы можете использовать следующий калькулятор.
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } σnСтандартная формула ошибки
Формула стандартной ошибки =σ =√n 0 = 0√0
Актуальность и использование
Стандартная ошибка имеет тенденцию быть высокой, если размер выборки для анализа мал. Следовательно, выборка всегда берется из большей совокупности, которая включает больший размер переменных. Это всегда помогает статистику определить достоверность среднего значения выборки относительно среднего значения генеральной совокупности.
Большая стандартная ошибка говорит статистику, что выборка неоднородна в отношении среднего значения генеральной совокупности. Относительно населения наблюдается большой разброс в выборке. Точно так же небольшая стандартная ошибка говорит статистику, что выборка однородна относительно среднего значения генеральной совокупности. Отсутствуют или незначительные различия в выборке относительно населения.
Не следует смешивать его со стандартным отклонением. Вместо этого следует рассчитать стандартное отклонение для всей совокупности. Стандартная ошибкаСтандартная ошибкаСтандартная ошибка (SE) — это метрика, которая измеряет точность выборочного распределения, обозначающего совокупность, с использованием стандартного отклонения. Другими словами, это мера дисперсии среднего значения выборки, связанная со средним значением генеральной совокупности, а не стандартное отклонение. С другой стороны, оно определяется для среднего значения выборки.
Стандартная формула ошибки в Excel
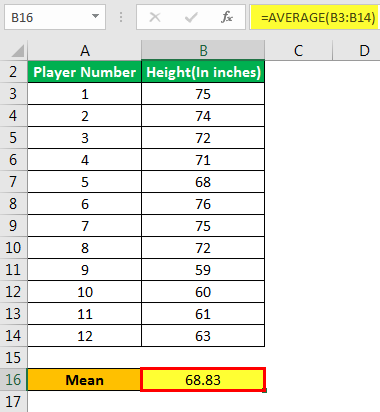
Теперь давайте возьмем пример Excel, чтобы проиллюстрировать концепцию стандартной формулы ошибки в шаблоне Excel ниже. Предположим, администрация школы хочет определить стандартную ошибку среднего значения роста футболистов.
Выборка состоит из следующих значений: –
Помогите администрации оценить стандартную ошибку среднего значения.
Шаг 1: Определите среднее значение, как показано ниже: –
Шаг 2: Определите стандартное отклонение, как показано ниже: –
Шаг 3: Определите стандартную ошибку среднего значения, как показано ниже: –
Следовательно, стандартная ошибка среднего значения для футболистов составляет 1,846 дюйма. Руководство должно заметить, что оно значительно велико. Таким образом, выборочные данные, взятые для анализа, неоднородны и имеют большую дисперсию.
Руководству следует либо исключить более мелких игроков, либо добавить игроков значительно выше, чтобы сбалансировать средний рост футбольной команды, заменив их людьми с меньшим ростом по сравнению с их сверстниками.
Рекомендуемые статьи
Эта статья была руководством по формуле стандартной ошибки. Здесь мы обсуждаем формулу для расчета среднего значения, стандартную ошибку, примеры и загружаемый лист Excel. Вы можете узнать больше из следующих статей: –
- Формула рентабельности EBITDA
- Формула валовой прибыли
- Формула относительного стандартного отклонения
- Формула погрешности