| Обноружение ошибок | Обноружение ошибок |  |
||||
| Исправление ошибок | Исправление ошибок |  |
||||
| Коррекция ошибок | Коррекция ошибок |  |
||||
| Назад | Назад |  |
||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = .
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.
ФГБОУ ВПО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ. М Е. ЕВСЕВЬЕВА»
Физико – математический факультет
Кафедра информатики и вычислительной техники
КУРСОВАЯ РАБОТА
ПРОБЛЕМЫ КОДИРОВАНИЯ ИНФОРМАЦИИ
Автор курсовой работы___________________________________ Д.А. Храмов
Направление подготовки 050100.62 Педагогическое образование
Профиль Математика. Информатика.
Руководитель работы
д.ф.–м.н., проф. каф. ИВТ______________________________ Е.В. Щенникова
Саранск 2013
Содержание
Введение……………………………………………………………………………3
1 Кодирование информации………………………………………………………5
1.1 Кодирование текстовой информации…………………………………5
1.2 Кодирование графической информации……………………….……..6
1.3 Кодирование звуковой информации………………………………….9
2 Шум и защита от шума. Теория кодирования К.Шеннона …………………11
3 Способы обнаружения ошибок с их последующим исправлением…………13
4 Основные понятия корректирующих кодов…………………………………15
4.1 Линейные и групповые коды…………………………………………17
4.2 Код Хэмминга………………………………………………………….21
Заключение……………………………………………………………………… 27
Список литературы………………………………………………………………28
Введение
Кодирование – процесс представления информации в виде кода. Под термином «кодирование», как правило, понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Кодирование в узком смысле – способ сделать сообщение непонятным для всех, кто не владеет ключом кода.
Первым, кто использовал кодирование двух символьной информации, был Готфрид Вильгельм Лейбниц. Он считал: «Вычисление с помощью двоек … является для науки основным и порождает новые открытия. При сведении чисел к простым началам, каковыми являются 0 и 1, везде появляется чудесный порядок». Но, к сожалению, эта система была забыта.
Первым теоретическое решение проблемы передачи данных по зашумленным каналам предложил
Клод Шеннон, основоположник статистической теории информации. Работая в Bell Labs, Шеннон написал работу «Математическая теория передачи сообщений» (1948), где показал, что если пропускная способность канала выше энтропии источника сообщений, то сообщение можно закодировать так, что оно будет передано без излишних задержек.
Переход от теории к практике стал возможен благодаря усилиям Ричарда Хэмминга, коллеги Шеннона по Bell Labs, получившего известность за открытие класса кодов «коды Хэмминга».
Хэмминг первым предложил «коды с исправлением ошибок» (Error-Correcting Code, ECC). Современные модификации этих кодов используются во всех системах хранения данных и для обмена между процессором и оперативной памятью. Один из их вариантов, коды Рида-Соломона применяются в компакт-дисках, позволяя воспроизводить записи без скрипов и шумов, вызванных царапинами и пылинками. Существует множество версий кодов, построенных «по мотивам» Хэмминга, они различаются алгоритмами кодирования и количеством проверочных битов. Особое значение подобные коды приобрели в связи с развитием дальней космической связи с межпланетными станциями.
Цель моей курсовой работы, является ознакомление с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Эта проблема в настоящее время относится к числу наиболее актуальных проблем, т.к. при обработке, передачи и хранении информации мы стремимся к повышению ее надежности.
Объект: процесс кодирования информации.
Задачи:
-
Проанализировать пособия по теории информации и информационной безопасности.
-
Выявить формы представления кодирования информации.
-
Обнаружение ошибок (проблем).
-
Методы и способы исправления ошибок.
1 Кодирование информации
Современный ПК может обрабатывать различную информацию (числовую, текстовую, звуковую и видео). Вся информация в компьютере представлена в двоичном коде, т.е. Используется алфавит мощностью два. Это связанно, прежде всего, с тем, что удобно представлять в виде последовательности электрических импульсов (импульс отсутствует — 0, импульс есть — 1). Логическая последовательность нулей и единиц называется, машинным кодом.
1.1 Кодирование текстовой информации
В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.
Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту, т. е. I = 1 байт = 8 бит. При помощи формулы, которая связывает между собой количество возможных событий К и количество информации I, можно вычислить сколько различных символов можно закодировать (считая, что символы — это возможные события): К = 2I 28 = 256, т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов.
Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ — 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные, при помощи одной таблицы не будут правильно отображаться в другой кодировке.
В большинстве случаев о перекодировке текстовых документов заботится пользователь, а специальные программы — конвертеры, которые встроены в приложения.
Начиная с 1997г. последние версии Microsoft Windows Office поддерживают новую кодировку Unicode, которая на каждый символ отводит по 2 байта, а поэтому, можно закодировать не 256 символов, а 65536 различных символов.
1.2 Кодирование графической информации
В середине 50-х годов для больших ЭВМ, которые применялись в научных и военных исследованиях, впервые в графическом виде было реализовано представление данных. В настоящее время широко используются технологии обработки графической информации с помощью ПК.
Особенно интенсивно технология обработки графической информации с помощью компьютера стала развиваться в 80-х годах. Графическую информацию можно представлять в двух формах: аналоговой или дискретной. Живописное полотно, цвет которого изменяется непрерывно — это пример аналогового представления, а изображение, напечатанное при помощи струйного принтера и состоящее из отдельных точек разного цвета — это дискретное представление. Чем большее количество цветов используется (т. е. точка изображения может принимать больше возможных состояний), тем больше информации несет каждая точка, а, значит, увеличивается качество кодирования. Создание и хранение графических объектов возможно в нескольких видах — в виде векторного, фрактального или растрового изображения.
Отдельным предметом считается 3D (трехмерная) графика, в которой сочетаются векторный и растровый способы формирования изображений.
Если говорить о кодировании цветных графических изображений, то нужно рассмотреть принцип декомпозиции произвольного цвета на основные составляющие. Применяют несколько систем кодирования: HSB, RGB и CMYK.
1) Модель HSB характеризуется тремя компонентами: оттенок цвета (Hue), насыщенность цвета (Saturation) и яркость цвета (Brightness). Можно получить большое количество произвольных цветов, регулируя эти компоненты.
2) Принцип метода RGB заключается в следующем: известно, что любой цвет можно представить в виде комбинации трех цветов: красного (Red, R), зеленого (Green, G), синего (Blue, B). Другие цвета и их оттенки получаются за счет наличия или отсутствия этих составляющих.
3) Принцип метода CMYK. Эта цветовая модель используется при подготовке публикаций к печати. Каждому из основных цветов ставится в соответствие дополнительный цвет (дополняющий основной до белого).
Различают несколько режимов представления цветной графики:
1) полноцветный (TrueColor);
2) HighColor;
3) индексный.
При полноцветном режиме для кодирования яркости каждой из составляющих используют по 256 значений (восемь двоичных разрядов), то есть на кодирование цвета одного пикселя (в системе RGB) надо затратить 8*3=24 разряда. Это позволяет однозначно определять 16,5 млн цветов. Это довольно близко к чувствительности человеческого глаза. При кодировании с помощью системы CMYK для представления цветной графики надо иметь 8*4=32 двоичных разрядов.
Режим HighColor — это кодирование при помощи 16-разрядных двоичных чисел, то есть уменьшается количество двоичных разрядов при кодировании каждой точки. Но при этом значительно уменьшается диапазон кодируемых цветов.
При индексном кодировании цвета можно передать всего лишь 256 цветовых оттенков. Каждый цвет кодируется при помощи восьми бит данных. Но так как 256 значений не передают весь диапазон цветов, доступный человеческому глазу, то подразумевается, что к графическим данным прилагается палитра (справочная таблица), без которой воспроизведение будет неадекватным: море может получиться красным, а листья — синими. Сам код точки растра в данном случае означает не сам по себе цвет, а только его номер (индекс) в палитре. Отсюда и название режима — индексный.
Соответствие между количеством отображаемых цветов (К) и количеством бит для их кодировки (а) находиться по формуле: К = 2а («Таблица 1») .
«Таблица 1»
|
А |
К |
Достаточно для |
|
4 |
24 = 16 |
|
|
8 |
28 = 256 |
Рисованных изображений типа тех, что видим в мультфильмах, но недостаточно для изображений живой природы |
|
16 (HighColor) |
216 = 65536 |
Изображений, которые на картинках в журналах и на фотографиях |
|
24 (TrueColor) |
224 = 16 777 216 |
Обработки и передачи изображений, не уступающих по качеству наблюдаемым в живой природе |
1.3 Кодирование звуковой информации
С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, микрофон и колонки, может записывать, сохранять и воспроизводить звуковую информацию. Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда, тем он громче для человека, чем больше частота сигнала, тем выше тон. Программное обеспечение компьютера в настоящее время позволяет непрерывный звуковой сигнал преобразовывать в последовательность электрических импульсов, которые можно представить в двоичной форме.
Процесс преобразования звуковых волн в двоичный код в памяти компьютера:
Звуковая волна →Микрофон → Переменный электрический ток → Аудиоадаптер →Двоичный код → Память компьютера
Процесс воспроизведения звуковой информации, сохраненной в памяти компьютера:
Память компьютера → Двоичный код → Аудиоадаптер → Переменный электрический ток → Динамик → Звуковая волна
Аудиоадаптер (звуковая плата)– специальное устройство, подключаемое к компьютеру, предназначенное для преобразования электрических колебаний звуковой частоты в числовой двоичный код при вводе звука и для обратного преобразования (из числового кода в электрические колебания) при воспроизведении звука.
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины.
Затем полученный код из регистра переписывается в оперативную память компьютера.
Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Частота дискретизации – это количество измерений входного сигнала за 1 секунду.
Разрядность регистра– число бит в регистре аудиоадаптера.
2 Шум и защита от шума. Теория кодирования К.Шеннона
Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи возникают по техническим причинам: плохое качество линии связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Например, при беседе по телефону, мы слышим шум и треск. В таких случаях необходима защита от шума. Способы защиты бывают самыми разными. Использование экранированного кабеля вместо «голого» провода; применение различных фильтров, отделяющих полезный сигнал от шума и т.п.
Клодом Шенноном была разработана специальная теория кодирования, дающая методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования К. Шеннона как раз и позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи часто применяется следующий прием борьбы с потерей информации. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета, и если она не совпадает с первоначальной, то передача данного пакета повторяется. Так происходит пока исходная и конечная контрольные суммы не совпадут.
3 Способы обнаружения ошибок с их последующим исправлением
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
-
обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
-
обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
-
Исправление ошибок применяется на физическом уровне.
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникших при передаче информации под влиянием помех, а так же при её хранении.
При записи в данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении её используют для того, чтобы обнаружить или исправить ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
Коды обнаружения ошибок в отличии от кодов исправляющих ошибки, могут только установить факт наличия ошибки.
Фактически любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
4 Основные понятия корректирующих кодов
Среди корректирующих кодов широко используются циклические коды, в ЭВМ эти коды применяются при последовательной передаче данных между ЭВМ и внешними устройствами, а также при передаче данных по каналам связи. Для исправления двух и более ошибок (d0 5) используются циклические коды БЧХ (Боуза — Чоудхури — Хоквингема), а также Рида-Соломона, которые широко используются в устройствах цифровой записи звука на магнитную ленту или оптические компакт-диски и позволяющие осуществлять коррекцию групповых ошибок. Способность кода обнаруживать и исправлять ошибки достигается за счет введений избыточности в кодовые комбинации, т.е. кодовым комбинациям из к двоичных информационных символов, поступающих на вход кодирующего устройства, соответствует на выходе последовательность из n двоичных символов (такой код называется (n, k) — кодом).
Если N0 = 2n-общее число кодовых комбинаций, а N = 2k — число разрешенных, то число запрещенных кодовых комбинаций равно
N0-N = 2n -2k.
При этом число ошибок, которое приводит к запрещенной кодовой комбинации равно (1).
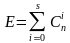
где S — кратность ошибки, т.е. количество искаженных символов в кодовой комбинации S = 0, 1, 2, …
Cni— сочетания из n элементов по i, вычисляемое, по формуле (2)
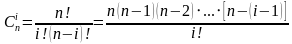
для S = 0; 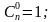
S = 1; 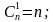
S = 2; 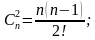
S= 3; 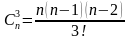
Для исправления S ошибок количество комбинаций кодового слова, составленного из m проверочных разрядов N = 2m, должно быть больше возможного числа ошибок (3), при этом количество обнаруживаемых ошибок в два раза больше, чем исправляемых
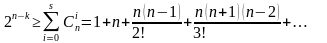
2m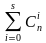
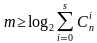
Для одиночной ошибки, как наиболее вероятной 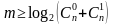
В зависимости от исходных данных кода (n или k) можно использовать
формулы (4).
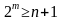
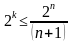
При этом, m = [log2(1+n)] или m = [log2 {(k+1)+ [log2(k+1)]}], где квадратные скобки обозначают округление до большего целого.
В таблице приведены соотношения между длиной кодовой комбинации и количеством информационных и контрольных разрядов для кода исправляющего одиночную ошибку, а также эффективность использования канала связи.
Для исправления двукратной ошибки (5).
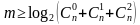
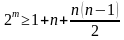
Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи.
Например, для кода (31, 26) скорость передачи информации равна
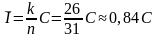
«Таблица 2»
|
n |
7 |
10 |
15 |
31 |
63 |
127 |
255 |
|
k |
4 |
6 |
11 |
26 |
57 |
120 |
247 |
|
m |
3 |
4 |
4 |
5 |
6 |
7 |
8 |
|
|
0,57 |
0,6 |
0,75 |
0,84 |
0,9 |
0,95 |
0,97 |
Как видно из таблицы , чем больше n, тем эффективнее используется канал.
4.1 Линейные и групповые коды
Линейным называется код, в котором проверочные символы представляют собой линейные комбинации информационных.
Групповым называется код, который образует алгебраическую группу по отношению операции сложения по модулю два.
Свойство линейного кода: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий этому коду.
Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами равно минимальному весу ненулевых векторов. Вес кодового вектора равен числу единиц в кодовой комбинации.
Групповые коды удобно задавать при помощи матриц, размерность которых определяется параметрами k и n. Число строк равно k, а число столбцов равно n = k+m.(6).
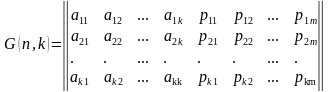
Коды, порождаемые этими матрицами, называются (n, k)-кодами, а соответствующие им матрицы порождающими (образующими, производящими). Порождающая матрица G состоит из информационной Ikk и проверочной Rkm матриц. Она является сжатым описанием линейного кода и может быть представлена в канонической (типовой) форме (7).
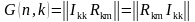
В качестве информационной матрицы удобно использовать единичную матрицу, ранг которой определяется количеством информационных разрядов (8).

Строки единичной матрицы представляют собой линейно-независимые комбинации (базисные вектора), т.е. их по парное суммирование по модулю два не приводит к нулевой строке.
Строки порождающей матрицы представляют собой первые k комбинаций корректирующего кода, а остальные кодовые комбинации могут быть получены в результате суммирования по модулю два всевозможных сочетаний этих строк.
Столбцы добавочной матрицы Rkm определяют правила формирования проверок. Число единиц в каждой строке добавочной матрицы должно удовлетворять условию r1 d0-1, но число единиц определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, и чем их больше, тем сложнее аппаратура.
Производящая матрица кода G(7,4) может иметь вид
Процесс кодирования состоит во взаимно — однозначном соответствии к-разрядных информационных слов — I и n-разрядных кодовых слов – с(9)
c=IG (9)
Например: информационному слову I=[1 0 1 0] соответствует кодовое слово (10).

При этом, информационная часть остается без изменений, а корректирующие разряды определяются путем суммирования по модулю два тех строк проверочной матрицы, номера которых совпадают с номерами разрядов, содержащих единицу в информационной части кода.
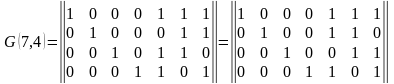
Процесс декодирования состоит в определении соответствия принятого кодового слова, переданному информационному. Это осуществляется с помощью проверочной матрицы H(n, k) (11).
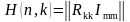
где RmkT -транспонированная проверочная матрица (поменять строки на столбцы); Imm— единичная матрица.
Для (7, 4)- кода проверочная матрица имеет вид (12).
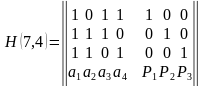
Между G(n ,k) и H(n, k) существует однозначная связь, т.к. они определяются в соответствии с правилами проверки, при этом для любого кодового слова должно выполняться равенство cHT= 0.
Строки проверочной матрицы определяют правила формирования проверок. Для (7, 4)-кода соответствует (13).
p1+a1+a2a4 = S1 ;
p2+a1+a2a3 = S2 ; (13)
p3+a1+a3a4 = S3 .
Полученный синдром сравниваем со столбцами матрицы и определяем разряд, в котором произошла ошибка, номер столбца равен номеру ошибочного разряда. Для исправления ошибки ошибочный бит необходимо проинвертировать.
4.2 Код Хемминга
Код Хэмминга относится к классу линейных кодов и представляет собой систематический код – код, в котором информационные и контрольные биты, расположены на строго определенных местах в кодовой комбинации.
Код Хэмминга, как и любой (n, k)- код, содержит к информационных и m = n-k избыточных (проверочных) бит.
Избыточная часть кода строится т.о. чтобы можно было при декодировании не только установить наличие ошибки но, и указать номер позиции, в которой произошла ошибка, а значит, и исправить ее, инвертировав значение соответствующего бита.
Существуют различные методы реализации кода Хэмминга и кодов которые являются модификацией кода Хэмминга. Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
-
По заданному количеству информационных символов — k, либо информационных комбинаций N = 2k , используя соотношения (14).
n = k+m, 2n (n+1)2k и 2m n+1 (14)
m = [log2 {(k+1)+ [log2(k+1)]}]
вычисляют основные параметры кода n и m.
2. Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону 2i,где i=1, 2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1 ) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно m = n-k. В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение — 0, в противном случае — 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n –чисел разрядностью – m или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до (2k –1) перечисленных в возрастающем порядке. Для m = 3 проверочная матрица имеет вид (15).
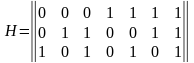
Количество разрядов m — определяет количество проверок («Таблица 3»).
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1, b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку — коэффициенты которые содержат 1 в третьем разряде и т.д.
«Таблица 3»
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) -разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.
В ЭВМ код Хэмминга чаще всего используется для обнаружения и исправления ошибок в ОП, памяти с обнаружением и исправлением ошибок ECCMemory (ErrorCheckingandCorrecting). Код Хэмминга используется как при параллельной, так и при последовательной записи. В ЭВМ значительная часть интенсивности потока ошибок приходится на ОП. Причинами постоянных неисправностей являются отказы ИС, а случайных изменение содержимого ОП за счет флуктуации питающего напряжения, кратковременных помех и излучений. Неисправность может быть в одном бите, линии выборки разряда, слова либо всей ИС. Сбой может возникнуть при формировании кода (параллельного), адреса или данных, поэтому защищать необходимо и то и др. Обычно дешифратор адреса встроен в микро схему и недоступен для потребителя. Наиболее часто ошибки дают ячейки памяти ЗУ, поэтому главным образом защищают записываемые и считываемые данные.
Наибольшее применение в ЗУ нашли коды Хэмминга с dmin=4, исправляющие одиночные ошибки и обнаруживающие двойные.
Проверочные символы записываются либо в основное, либо специальное ЗУ. Для каждого записываемого информационного слова (а не байта, как при контроле по паритету) по определенным правилам вычисляется функция свертки, результат которой разрядностью в несколько бит также записывается в память. Для 16-ти разрядного информационного слова используется 6 дополнительных бит (32 — 7 бит, 64 – 8 бит). При считывании информации схема контроля («Рис. 1»), используя избыточные биты, позволяет обнаружить ошибки различной кратности или исправить одиночную ошибку. Возможны различные варианты поведения системы:
-
автоматическое исправление ошибки без уведомления системы;
-
исправление однократной ошибки и уведомление системы только о многократных ошибках;
-
не исправление ошибки, а только уведомление системы об ошибках;
Модуль памяти со встроенной схемой исправления ошибок – EOS 72/64 (ECConSimm). Аналог микросхема к 555 вж 1 -это 16 разрядная схема с обнаружением и исправлением ошибок (ОИО) по коду Хэмминга G(22, 16), использование которой позволяет исправить однократные ошибки и обнаружить все двух кратные ошибки в ЗУ.
Избыточные (контрольные) разряды позволяют обнаружить и исправить ошибки в ЗУ в процессе записи и хранения информации.
В составе ВЖ-1 используются 16 информационных и 6 контрольных разрядов. (DB — информационное слово, CB — контрольное слово).
При записи осуществляется формирование кода, состоящего из 16 информационных и 6 контрольных разрядов, представляющих результат суммирование по модулю 2 восьми информационных разрядов в соответствии с кодом Хэмминга. Сформированные контрольные разряды вместе с информационными поступают на схему и записываются в ЗУ.
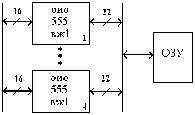
«Рис. 1» — схема контроля
При считывании шестнадцатиразрядное слово декодируется, восстанавливаясь вместе с 6 разрядным словом контрольным, поступают на схему сравнения и контроля. Если достигнуто равенство всех контрольных разрядов и двоичных слов, то ошибки нет.
Любая однократная ошибка в 16 разрядном слове данных изменяет 3 байта в 6 разрядном контрольном слове. Обнаруженный ошибочный бит инвертируется.
Заключение
Цель моей работы достигнута: я познакомился с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Рассмотрел циклические коды, исправляющие более 2 ошибок (к ним относятся коды БЧХ (Боуза — Чоудхури — Хоквингема) и Рида-Соломона) и линейные коды (коды Хемминга). Все они основываются на избыточности информации.
Научились находить эту избыточность с помощью формул. Узнал, что любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
Познакомился с различными способами кодирования различных видов информации: текстовой, графической и звуковой.
Список литературы
-
Недвоичные арифметические корректирующие коды, проблемы передачи информации / В.М. Гриценко — 4-е изд. – 1969. – 19 – 27 с.
-
Помехоустойчивые коды в системах связи / Б.М. Золотник — M.: Радио и связь, 1989.—232 c.
-
Информационная безопасность. Лабораторный практикум: учебное пособие / А.В. Бабаш, Е.К. Баранова, Ю.Н. Мельникова. — М.: КНОРУС, 2012. – 136 с.
-
Теория передачи сигналов / Кловский Д.Д. — M.: Cвязь, 1984.
-
Цифровое кодирование звуковых сигналов / Ковалгин Ю.A., Вологдин Э.И. — Изд-во Kорона-принт, 2004. – 240с.
-
Курс теории информации / Колесников B.Д., Полтырев Г.Ш. — M.: Наука, 1982. 416 с.
-
Микропроцессорные кодеры и декодеры / В.М. Муттер, Г.A. Петров и др.—M.: Радио и связь, 1991.—184 с.
-
Экономное кодирование дискретной информации / Семенюк В. В. – СПб: СПбГИТМО (ТУ), 2001. – 115 с.
Программирование — это умная работа и поиск эффективных способов создания полезного программного обеспечения. При создании программ, веб-приложений или мобильных приложений принципы программирования остаются неизменными.
При первом изучении кода важно понимать хорошие и плохие привычки. Знание ошибок, которые делают программисты, и то, как их избежать, может помочь вам создать лучшую основу для программирования. Вот 10 очень распространенных ошибок, которых следует избегать.
1. Повторяющийся код
Не повторяйте себя — это один из основных принципов программирования. что вы встретите, как вы узнаете. Это часто сокращается до СУХОГО, и код, который написан с использованием этого принципа, называется СУХОЙ код.
Повторение кода — это легкая ловушка, в которую часто попадают, и часто требуется некоторый обзор, чтобы понять, сколько кода повторяется. Как хорошее практическое правило, если вы копируете и вставляете код, он, вероятно, повторяется и должен быть изменен.
Получите удобство, используя циклы и функции, чтобы сделать вашу работу за вас, и эта проблема исчезнет.
2. Неверные имена переменных
Переменные имеют важное значение в программировании независимо от того, на каком языке вы работаете. Поскольку они широко используются, важно иметь хорошие привычки именования переменных.
Переменные должны быть названы точно и аккуратно. Избегайте использования общих терминов, которые ничего не значат. Быстро и легко собрать что-то вместе, но когда вам нужно вернуться к своему коду позже, становится намного сложнее понять, что происходит.
Допустим, вы пишете программу, которая использует процентную ставку для расчета. Вы пишете переменную для использования в программе.
let rate = 0.1; Все, что мы действительно знаем об этой переменной, это то, что это показатель. Какой тариф?
Код будет работать просто отлично, но сложно сказать, что здесь происходит.
Вместо этого назовите ваши переменные более четко.
let interestRate = 0.1;
3. Не используя комментарии
Используйте комментарии! Комментарии — это документация вашего кода. Это лучший способ описать, что именно происходит в вашем коде по мере его роста. Конечно, кажется, немного больше работы, чтобы объяснить ваш код, но вы будете благодарить себя позже.
Написать блестящую функцию? Напишите комментарий о том, что он делает. Создание нового шаблона объекта для объектно-ориентированного программирования? Разбейте это комментарием. Комментарии используются на каждом языке, и они есть по причине.
Комментарии делают ваш код чище, легче ориентироваться и делают вас героем следующего разработчика, который, возможно, должен будет работать над вашим проектом.
4. Языковая перегрузка
Проблема, которая, кажется, перегружает растущих разработчиков, — это заграждение новых языков и технологий. Сообщества разработчиков онлайн полны вопросов о выборе языка.
Должен ли я писать в своем приложении на JavaScript или использовать фреймворк, такой как Node.JS или Express? Должен ли я использовать Python, Scala или Ruby для разработки? C или C ++ или C #? Какие рамки лучше? Должен ли я изучить MongoDB или SQL или SQLite для базы данных? Является ли этот язык устаревшим ??
Не беспокойся об этом.
Шаг назад, сосредоточиться на основах. Языки приходят и уходят, но самые успешные разработчики решают проблемы. Постройте свое программирование на алгоритмическом мышлении, и все остальное станет на свои места.
Эти технологии — всего лишь инструменты, и если вы знаете, в чем заключаются проблемы, вы будете знать, какой инструмент использовать для их решения.
5. Не резервное копирование кода
Неспособность выработать правильные привычки для защиты вашего кода разочаровывает новых разработчиков и губительна для опытных.
Как программисту, очень важно постоянно сохранять и резервировать свою работу. Это ничем не отличается от работы с важным документом или таблицей, которая часто сохраняется.
Узнайте, как управлять файлами с помощью Git. Любой контроль версий на самом деле, программное обеспечение, которое вы используете, не так важно, как умение правильно его использовать. Вы не хотите терять важные изменения, если ваш компьютер выходит из строя или выходит из строя сеть.
6. Сложный код
Кодирование не является тестом IQ. Это не проблема, чтобы увидеть, кто может использовать самые сложные функции или впечатляющие файлы. Код должен быть написан в духе эффективного решения проблем. Простой код легче писать, легче поддерживать и легче управлять.
Чтобы быть понятным, простой код не означает использование ярлыков. Простой код означает понимание сути проблемы, которую вы хотите решить, и эффективное ее решение.
7. Не задавая вопросов
Программирование трудно делать хорошо, а совершенствование означает постоянное изучение новых вещей. Лучшее, что вы можете сделать, — это читать и изучать программирование, чтобы стать лучше, но когда вам нужно какое-то дополнительное руководство, не бойтесь задавать вопросы.
Задавать вопросы могут быть пугающими, но большинство опытных программистов рады поделиться знаниями и идеями.
Просто убедитесь, что вы сделали свое исследование и приложили к нему реальные усилия. Опытные разработчики с большей вероятностью будут наставлять вас, если увидят, что вы посвятили себя обучению. Возможно, ведите журнал программирования, чтобы стать лучше. лучшим , отслеживая важные вопросы и ответы.
8. Не планировать заранее
Написание эффективного программного обеспечения начинается с хорошего планирования и дизайна. Если вы хотите построить дом, вы должны составить план до начала строительства. Программирование ничем не отличается.
Прежде чем написать хотя бы одну строку кода, определите, чего вы на самом деле хотите достичь. Знайте, в чем проблема, как вы хотите ее решить. Если вы попытаетесь выяснить проблемы во время написания кода, вы можете упустить правильные решения.
Отделите решение проблем от кодирования и жизнь хороша.
9. Не делать перерывов
Сделай перерыв, правда! Программирование ментально обременительно, и долгие часы, потянув ваш мозг до предела, в конечном итоге измотают вас. Даже хуже, чем усталость, вы можете страдать от головных болей или болей в шее, которые являются признаками компьютерного напряжения глаз.
Когда вы попали в стену, пришло время сделать перерыв. Отойди от экрана немного и сделай то, что тебе нравится. Прочитайте книгу, отправляйтесь на улицу, отправляйтесь в поход, поужинайте, все, что вас увлекает.
Вы будете морально обновлены, и когда вы вернетесь, вы можете найти новую перспективу в вашем коде.
10. Не веселиться
Программирование может быть сложным, разочаровывающим, а иногда и совершенно бесполезным. Убедитесь, что вам нравятся мелочи, которые вам нравятся в кодировании, и не забудьте немного повеселиться.
Занимаетесь ли вы этим, решая сложные задачи, создавая красивые дизайны или просто изучая новые навыки, используйте то, что вы любите, чтобы продолжать работать. В кодировании есть что любить, так что вдохновляйтесь! Будьте взволнованы, чтобы сделать что-то новое, и доведите это до конца.
Не делайте эти ошибки программирования
Легко попасть в рутину, либо пытаясь понять, что должно быть простым, либо пытаясь вспомнить, что делает какой-то код. В любом случае, избегайте ошибок, и ваш код улучшится.
Все еще борется? Не забывайте, что есть множество увлечений для программистов, которые не связаны с кодом для программистов, которые не привлекают программистов Кодекс для программистов, которые не задействуют код
Ошибка — кодирование
Cтраница 1
Ошибка кодирования равна 1 — j — для любого п, и поэтому при е 1 — — — — 27 те Рема верна.
[1]
Алгоритмические ошибки и ошибки кодирования, связанные с некорректной формулировкой и реализацией алгоритмов программным путем.
[2]
Необходимо доказать, что ошибка кодирования, близкая к е, получается при выборе аппроксимирующего множества Тп, содержащего М-2 пН элементов, где Я ( е) — — е-энтропия ансамбля X при вероятностном критерии качества.
[3]
Это позволяет уменьшить число ошибок кодирования. Сессии способны положительно повлиять как на группу проектировщиков, так и на изучающих опыт этой группы. При этом предъявлять для изучения результаты своей работы должны все проектировщики, от самых старших до самых младших.
[4]
Большое значение рефлексного кода заключается в его свойстве минимизировать ошибки кодирования; это его свойство связано с тем фактом, что при переходе от одного уровня к следующему изменяется только одна цифра.
[5]
Выделяемые при отладке ошибки могут быть различного характера: ошибки кодирования, алгоритмизации и логики программы, а также из-за неправильного понимания требований задачи или функций машины, неточного выполнения требований системных спецификаций.
[6]
Если эти три изображения кодируются отдельно друг от друга, ошибка кодирования и ошибка в канале будут значительно влиять на визуальное качество реконструированного цветного изображения, что связано со свойствами цветового восприятия человека.
[8]
Хотя некоторые ошибки могут происходить в результате недостатков вычислительных алгоритмов, ошибок кодирования программ и ошибок округления, и это действительно случается время от времени, все же большинство ошибок в БД обусловлены неправильным вводом.
[9]
Ошибки при передаче информации происходят из-за: шума в канале ( атмосферные и технические помехи), ошибки кодирования и декодирования. Теория информации изучает, в частности, способы минимизации количества таких ошибок.
[10]
При этом вероятность повторения одинаковой ошибки у обоих кодировщиков ничтожно мала, и сопоставляя результаты их кодироваиня, удается найти практически все ошибки кодирования.
[11]
Программа, написанная на машинном языке ( или, как говорят, в машинных кодах), содержит минимум избыточной информации, на основе которой можно было бы обнаружить формальные ошибки кодирования.
[12]
Передача серии данных может быть асинхронной или синхронной, биты, составляющие символ, могут быть кодированы в NRZ ( nonreturn to zero — без возвращения к нулю) или, предпочтительно, в манчестерском коде и дополнены кодами распознавания и исправления ошибок кодирования символа.
[13]
Дополнительно могут быть перечислены наименования вентилей, которые в свою очередь питает он сам. Если это сделано, то возможна проверка ошибок кодирования сравнением двух заданных таким образом описаний схемы. Она говорит о том, что А2 является первым вентилем контура обратной связи, последний вентиль которого есть Rl ( RI вполне может питать и другие вентили, не являющиеся первыми вентилями в контурах обратной связи, для которых R1 — последний вентиль в контуре. Для таких вентилей звездочка обычно опускается.
[15]
Страницы:
1
2
Какие существуют методы анализа и локализации ошибки
Под тестированием следует понимать процесс исполнения программы с целью обнаружения ошибок, в качестве которых принимается любое отклонение от эталонов. Хорошим считается тест, который имеет высокую вероятность обнаружения еще не выявленных ошибок.
Под отладкой понимается процесс, позволяющий получить программу, функционирующую с требуемыми характеристиками в заданной области входных данных. Таким образом, в результате отладки программа должна соответствовать некоторой фиксированной совокупности правил и показателей качества, принимаемой за эталонную для данной программы.
Существует три основных способа тестирования:
Алгоритмическое тестирование применяется для контроля этапов алгоритмизации и программирования. Проектируются тесты и начинаются готовиться эталонные результаты на этапе алгоритмизации, а используются они на этапе отладки.
Функциональное или аналитическое тестирование
Аналитическое тестирование служит для контроля выбранного метода решения задачи, правильности его работы в выбранных режимах и с установленными диапазонами данных. Тесты проектируют и начинают готовить сразу после выбора метода, а используют их на последнем этапе отладки, в ходе тестирования, наряду со сверкой на совпадение, применяются и качественные оценки результатов.
Содержательное тестирование служит для проверки правильности постановки задачи. Для контроля при этом используются, как правило, качественные оценки и статистические характеристики программы, физический смысл полученных результатов и т.п. в проведении содержательного тестирования, принципы которого формулируются в техническом задании, самое активное участие должны принимать заказчики или идущие пользователи программы.
Содержательные и аналитические тесты проверяют правильность работы программы в целом или крупных ее частей, в то время как алгоритмические тесты в первую очередь должны проверять работу отдельных блоков или операторов программы.
Тот вид контроля, который рассматривался выше, можно назвать тестированием основных функциональных возможностей программы — основной тест.
Этот тест затрагивает работу программы в самой минимальной степени. Обычно тест служит для проверки правильности выполнения самых внешних функций программы, например, обращения к ней и выхода из нее.
Тест граничных значений
Тест проверяет работу программы для граничных значений параметров, определяющих вычислительный процесс. Часто для граничных значений параметра работа программы носит особый характер, который, тем самым, требует и особого контроля.
Тест проверяет реакцию программы на возникновение разного рода аварийных ситуаций в программе, в частности, вызванных неправильными исходными данными. Другими словами, проверяется диагностика, выдаваемая программой, а также окончание ее работы или, может быть, попытка исправления неверных исходных данных.
Локализация ошибок
После того, как с помощью тестов (или каким либо другим путем) установлено, что в программе или в конкретном ее блоке имеется ошибка, возникает задача ее локализации, то есть установления точного места в программе, где находится ошибка.
Процесс локализации ошибок состоит из следующих трех компонент:
Получение на машине тестовых результатов.
Анализ тестовых результатов и сверка их с эталонными.
Выявление ошибки или формулировка предположения о характере и месте ошибки в программе.
Технология отладки автоматизированного рабочего места
При отладке программы использовались следующие методы контроля и локализации ошибок: просмотр текста программы с целью обнаружения явных синтаксических и логических ошибок и трансляция программы (транслятор выдает сообщения об обнаруженных им ошибках в тексте программы).
Тестирование проводилось посредством ввода исходных данных, с дальнейшей их обработкой, выводом результатов на экран. Результаты работы программы сравнивались с требованиями в техническом задании.
1) Отладка программы производилась следующим образом:
2) Запуск программы с набором тестовых входных данных и выявление наличия ошибок.
3) Выделение области программы, в которой может находиться ошибка.
4) Просмотр листинга программы с целью возможного визуального обнаружения ошибок. В противном случае — установка контрольной точки примерно в середине выделенной области.
Новая прогонка программы. Если работа программы прервалась до обработки контрольной точки, значит, ошибка произошла раньше. Контрольная точка переносится, и процесс отладки возвращается к шагу 2.
Если контрольная точка программы была обработана, то далее следует изучение значений стека, переменных и параметров программы с тем, чтобы убедиться в их правильности. При появлении ошибки — новый перенос контрольной точки и возврат к шагу 2.
В случае если ошибка не была обнаружена, далее выполнение программы производится покомандно, с контролем правильности выполнения переходов и содержимого регистров и памяти в контрольных точках. При локализации ошибки, она исправляется, и процесс возвращается к шагу 1.
В данном разделе были рассмотрены вопросы разработки, отладки и тестирования программных продуктов. Было приведено обоснование необходимости и важности этапа отладки в процессе разработки программного обеспечения, даны краткие описания основных способов отладки и тестирования.
В отношении разработанной в специальной части программы было дано описание алгоритма, использовавшегося при ее отладки и тестировании. Представлено обоснование выбора языка программирования.
7. Локализация ошибок
После того, как с помощью контрольных тестов (или каким либо другим путем) установлено, что в программе или в конкретном ее блоке имеется ошибка, возникает задача ее локализации, то есть установления точного места в программе, где находится ошибка.
Процесс локализации ошибок состоит из следующих трех компонент:
1. Получение на машине тестовых результатов.
2. Анализ тестовых результатов и сверка их с эталонными.
3. Выявление ошибки или формулировка предположения о характере и месте ошибки в программе.
По принципам работы средства локализации разделяются на 4 типа :
1. Аварийная печать.
2. Печать в узлах.
АВАРИЙНАЯ ПЕЧАТЬ осуществляется один раз при работе отлаживаемой программы, в момент возникновения аварийной ситуации в программе, препятствующей ее нормальному выполнению. Тем самым, конкретное место включения в работу аварийной печати определяется автоматически без использования информации от программиста, который должен только определить список выдаваемых на печать переменных.
ПЕЧАТЬ В УЗЛАХ включается в работу в выбранных программистом местах программы; после осуществления печати значений данных переменных продолжается выполнение отлаживаемой программы.
СЛЕЖЕНИЕ производится или по всей программе, или на заданном программистом участке. Причем слежение может осуществляться как за переменными (арифметическое слежение), так и за операторами (логическое слежение). Если обнаруживается, что происходит присваивание заданной переменной или выполнение оператора с заданной меткой, то производится печать имени переменной или метки и выполнение программы продолжается. Отличием от печати в узлах является то, что место печати может точно и не определяться программистом (для арифметического слежения); отличается также и содержание печати.
ПРОКРУТКА производится на заданных участках программы, и после выполнения каждого оператора заданного типа (например, присваивания или помеченного) происходит отладочная печать.
По типам печатаемых значений (числовые и текстовые или меточные) средства разделяются на арифметические и логические.
7.2. Классификация средств локализации ошибок
Ниже дана классификация средств локализации.
ТИПЫ СРЕДСТВ ЛОКАЛИЗАЦИИ ОШИБОК :
СРЕДСТВА ЛОКАЛИЗАЦИИ:
1. Аварийная печать (арифметическая).
1.1. Специальные средства языка.
1.2. Системные средства.
2. Печать в узлах (арифметическая).
2.1. Обычные средства языка.
2.2. Специальные средства языка.
3. Слежение (специальные средства).
4. Прокрутка (специальные средства).
8. Технология отладки программы автоматизации учета движения товаров на складе малого предприятия
При отладке программы использовались следующие методы контроля и локализации ошибок (обзор методов см. в теоретической части раздела) :
1. Просмотр текста программы и прокрутка с целью обнаружения явных синтаксических и логических ошибок.
2. Трансляция программы (транслятор выдает сообщения об обнаруженных им ошибках в тексте программы).
3. Тестирование. Тестирование проводилось посредством ввода исходных данных, с дальнейшей их обработкой, выводом результатов на печать и экран. Результаты работы программы сравнивались заданными в техническом задании.
4. При локализации ошибок преимущественно использовалась печать в узлах, которыми являлись в основном глобальные переменные, переменные, используемые при обмене данными основной программы с подпрограммами.
Отладка программы производилась по следующему алгоритму :
1. Прогонка программы с набором тестовых входных данных и выявление наличия ошибок.
2. Выделение области программы, в которой может находиться ошибка. Просмотр листинга программы с целью возможного визуального обнаружения ошибок. В противном случае — установка контрольной точки примерно в середине выделенной области.
3. Новая прогонка программы. Если работа программы прервалась до обработки контрольной точки, значит, ошибка произошла раньше. Контрольная точка переносится, и процесс отладки возвращается к шагу 2.
4. Если контрольная точка программы была обработана, то далее следует изучение значений регистров, переменных и параметров программы с тем, чтобы убедиться в их правильности. При появлении ошибки — новый перенос контрольной точки и возврат к шагу 2.
5. В случае не обнаружения ошибки продолжение выполнения программы покомандно, с контролем правильности выполнения переходов и содержимого регистров и памяти в контрольных точках. При локализации ошибки она исправляется и процесс возвращается к шагу 1.
В качестве тестовых входных данных использовалась последовательность частотных выборок, генерируемых имитатором в режиме 1. (Каждому интервалу соответствует фиксированное значение выборок.)
Итоговый тест по дисциплине «Поддержка и тестирование программных модулей»
Является ли программа аналогом математической формулы?
Варианты ответов
- Да
- Нет
- Математические формулы и программы не сводятся друг к другу
Вопрос 2
Какие подходы используются для обоснования истинности программ?
Варианты ответов
- использование аналогий
- эксперимент над программой
- доказательство программы
- формальный и интерпретационный
Вопрос 3
Отметьте верные утверждения
Варианты ответов
- тестирование – процесс поиска ошибок
- в фазу тестирования входят поиски и исправление ошибок
- отладка – процесс локализации и исправления ошибок
Вопрос 4
Зачем нужна спецификация тестирования?
Варианты ответов
- для формирования команды тестировщиков
- для разработки тестового набора
- для понимания смысла программы
Вопрос 5
Варианты ответов
- выполнение программы в уме
- пошаговое выполнение
- метод контрольных точек и анализа трасс
Вопрос 6
Зачем нужен Log-файл?
Варианты ответов
- для изучения результатов тестирования в режиме on-line
- для фиксации результатов прогона test-suite
- для записи комментариев после прогона тестов
Вопрос 7
Варианты ответов
- разработка тестового набора
- прогон программы на тестовом наборе
- доказательство правильности программы
- анализ результатов тестирования
Вопрос 8
Варианты ответов
- определение областей эквивалентности входных параметров
- анализ покрытия тестами всех возможных случаев поведения
- проверка граничных значений
Вопрос 9
Что такое управляющий граф программы (УГП)?
Варианты ответов
- множество операторов программы.
- граф, вершины которого кодируют операторы программы, а дуги — управления (порядок исполнения) операторов
- множество операторов управления
Вопрос 10
Варианты ответов
- множество связанных дуг УГП
- последовательность вершин и дуг УГП с фиксированными начальной и конечной вершиной
- последовательность ветвей УГП с фиксированными начальной вершиной первой ветви и конечной вершиной последней ветви пути
Вопрос 11
Варианты ответов
- нереализуемый путь недоступен при корректном исполнении программы
- нереализуемый путь недоступен всегда
- нереализуемый путь доступен при сбое
- нереализуемый путь доступен при реализации недопустимых состояний переменных программы
Вопрос 12
Возможно ли тестирование программы на всех допустимых значениях параметров?
Варианты ответов
- да, всегда
- никогда
- возможно в отдельных случаях
Вопрос 13
Какие предъявляются требования к идеальному критерию тестирования?
Варианты ответов
- достаточность
- достижимость
- полнота
- проверяемость
Вопрос 14
Какие классы критериев тестируемости известны
Варианты ответов
- структурные критерии
- мутационные критерии
- функциональные критерии
- сценарные критерии
- стохастические критерии
Вопрос 15
Варианты ответов
- сценарный критерий
- такого критерия не существует
- критерий «черного ящика»
Вопрос 16
Варианты ответов
- критерий тестирования команд
- критерий тестирования ветвей
- критерий тестирования циклов
- критерий тестирования путей
Вопрос 17
Варианты ответов
- не проверяется соответствие со спецификацией
- не проверяется соответствие со спецификацией, не зафиксированное в структуре программы
- не проверяются ошибки в структурах данных
Вопрос 18
Варианты ответов
- тестирование пунктов спецификации
- тестирование классов входных данных
- тестирование классов выходных данных
- тестирование функций
- тестирование правил
Вопрос 19
Варианты ответов
- не проверяется соответствие со спецификацией
- не проверяются ошибки, требования к которым не зафиксированы в спецификации
- не проверяются ошибки в структурах данных, требования к которым не зафиксированы в спецификации
Вопрос 20
Варианты ответов
- создание программ-мутантов на основе изменения модульной структуры основной программы
- создание программ-мутантов с функциональными дефектами
- оценка числа ошибок в программе на основе искусственно внесенных мелких ошибок
Вопрос 21
Варианты ответов
- оценка проекта интегрирует оценки оттестированности модулей
- оценка проекта может вычисляться инкрементально
- в результате получаем наихудшую оценку оттестированности
- в результате получаем наилучшую оценку оттестированности
Вопрос 22
Какие существуют разновидности уровней тестирования?
Варианты ответов
- модульное
- интеграционное
- структурное
- системное
- регрессионное
Вопрос 23
Какие задачи у модульного тестирования?
Варианты ответов
- выявление ошибок при вызове модулей
- выявление ошибок взаимодействия модуля с окружением
- выявление локальных ошибок реализации алгоритмов модулей
Вопрос 24
На основе каких принципов строятся тесты для модульного тестирования?
Варианты ответов
- анализ потоков управления модуля
- анализ потоков данных модуля
- анализ покрытия в соответствии с заданными структурными критериями
Вопрос 25
Варианты ответов
- построение УГП (управляющего графа программы)
- выбор тестовых путей
- генерация тестов, соответствующих выбранным тестовым путям
Вопрос 26
Варианты ответов
- статические
- динамические
- методы реализуемых путей
Вопрос 27
Варианты ответов
- Регрессионное тестирование
- монолитное тестирование
- нисходящее тестирование
- восходящее тестирование
Вопрос 28
Варианты ответов
- необходимость разработки заглушек
- параллельная разработка эффективных модулей
- необходимость разработки среды управления очередностью вызовов модулей
- необходимость разработки драйверов
Вопрос 29
Варианты ответов
- тесты оперируют пользовательским или другими внешними интерфейсами
- структура проекта тестируется на уровне подсистем
- тестированию подлежит система в целом
- тестирование осуществляется по методу «черного ящика»
Вопрос 30
Варианты ответов
- выявление дефектов в функционировании приложения или в работе с ним
- выявление дефектов использования ресурсов
- выявление несовместимости с окружением
- выявление непредусмотренных сценариев применения или использования непредусмотренных комбинаций данных
Вопрос 31
Варианты ответов
- перетестирование предусматривает только контроль частей приложения, связанных с изменениями
- выбор между полным и частичным перетестированием и пополнением тестовых наборов
- регрессионное тестирование является подмножеством системного тестирования
Вопрос 32
Какие типы дефектов выявляются при системном и регрессионном тестировании
Программные ошибки. Методы отладки
Прежде всего определимся с некоторыми понятиями, связанными с отладкой программного обеспечения.
Программная ошибка — это расхождение между программой и ее спецификацией, причем тогда и только тогда, когда спецификация существует и она правильна. Также можно определить, что программная ошибка — это ситуация, когда программа не делает того, что пользователь от нее вполне обоснованно ожидает.
Отладкой называют процесс локализации и исправления ошибок, обнаруженных при тестировании программного обеспечения.
Локализация — это определение оператора/операторов программы, выполнение которого вызвало нарушение вычислительного процесса.
Для исправления ошибки необходимо определить ее причину, т.е. определить оператор или фрагмент, содержащие ошибку. Причины ошибок могут быть и очевидными, и очень глубоко скрытыми.
В соответствии с этапом обработки, на котором появляются ошибки, различают ошибки компиляции, ошибки компоновки, ошибки выполнения (рис. 5.1) [7].
Рис. 5.1. Группы программных ошибок
Ошибки компиляции — это синтаксические ошибки, фиксируемые компилятором (транслятором, интерпретатором). Ошибки компиляции являются самыми простыми, так как синтаксис языка, как правило, строго формализован, и ошибки сопровождаются подробным комментарием с указанием местоположения ошибки. Чем лучше формализованы правила синтаксиса языка, тем больше ошибок из общего количества может обнаружить компилятор и, соответственно, меньше ошибок возникнет на следующих этапах.
Ошибки компоновки — ошибки, обнаруженные компоновщиком (редактором связей) при объединении модулей программы. Ошибки компоновки связаны с проблемами, обнаруженными при разрешении внешних ссылок. Например, предусмотрено обращение к подпрограмме другого модуля, а при объединении модулей данная подпрограмма не найдена или не стыкуются списки параметров.
Ошибки выполнения — ошибки, обнаруженные операционной системой, аппаратными средствами или пользователем при выполнении программы. Ошибки выполнения являются самыми непредсказуемыми. Некоторые из них обнаруживаются и документируются операционной системой. Они могут иметь разную природу и поэтому по-разному проявляться:
- • появление сообщения об ошибке, например, деление на ноль, нарушение адресации, переполнение разрядов и т.п.;
- • появление сообщения об ошибке, обнаруженной операционной системой, например при попытке записи на защищенные устройства памяти, при ссылке на отсутствующий файл и т.п.;
- • «зависание» компьютера (иногда для продолжения работы необходима его перезагрузка);
- • несовпадение полученных результатов с ожидаемыми.
Причины ошибок выполнения очень разнообразны, а потому их
сложно локализовать. Все возможные причины ошибок выполнения можно разделить на следующие группы:
- • ошибки определения данных;
- • логические ошибки;
- • ошибки накопления погрешностей.
Ошибки определения данных (неверное определение исходных данных) возникают при выполнении операций ввода-вывода: ошибки передачи, ошибки преобразования, ошибки перезаписи, ошибки данных. Использование специальных технических средств и программирование с защитой от ошибок позволяют обнаружить и предотвратить только часть этих ошибок.
Логические ошибки имеют разную природу и могут следовать из ошибок, допущенных при проектировании, например при выборе методов, разработке алгоритмов или определении структуры данных (классов), а могут быть непосредственно внесены при кодировании модуля. К ошибкам кодирования относятся:
- • ошибки некорректного использования переменных, например неудачный выбор типов данных, использование переменных до их инициализации, использование индексов, выходящих за границы определения массивов, нарушения соответствия типов данных и т.п.;
- • ошибки вычислений, например некорректная работа с переменными, некорректное преобразование типов данных в процессе вычислений и т.п.;
• ошибки взаимодействия модулей, т.е. межмодульного интерфейса, например нарушение типов и последовательности при передаче параметров, несоблюдение единства единиц измерения формальных и фактических параметров, нарушение области действия локальных и глобальных переменных.
Возможны и другие ошибки кодирования, например неправильная реализация логики программы при кодировании, игнорирование особенностей или ограничений конкретного языка программирования.
Ошибки накопления погрешностей возникают в результате накопления погрешностей результатов числовых вычислений, например при некорректном отбрасывании дробных цифр чисел, при некорректном использовании приближенных методов вычислений и т.п.
Процесс отладки требует от разработчика глубоких знаний специфики среды и языка программирования, используемых технических средств, операционной системы. На сложность отладки оказывают влияние следующие факторы:
- • опосредованное проявление ошибок;
- • возможность взаимного влияния ошибок;
- • возможность получения внешне одинаковых проявлений разных ошибок;
- • стохастические ошибки, которые могут не проявиться от запуска к запуску;
- • может аннулироваться или измениться внешнее проявление ошибок при внесении некоторых изменений в программу, например, при включении в программу диагностических фрагментов. Отладка программы всегда предполагает обдумывание и логическое осмысление всей имеющейся информации об ошибке. Большинство ошибок можно обнаружить, тщательно анализируя текст программы и результаты тестирования.
Методы отладки программного обеспечения можно классифицировать следующим образом [7]:
- • метод ручного тестирования;
- • метод индукции;
- • метод дедукции;
- • метод обратного прослеживания.
Метод ручного тестирования — самый простой и естественный способ отладки программы. При обнаружении ошибки необходимо выполнить тестируемую программу вручную, используя тестовый набор, при работе с которыми была обнаружена ошибка. Метод эффективен, но не применим для больших программных систем и программ со сложными вычислениями. Этот метод часто используют как составную часть других методов отладки.
Метод индукции предусматривает подробный анализ проявления ошибки. Это могут быть неверные результаты вычислений или сообщение об ошибке. Если компьютер просто «зависает», то место проявления ошибки в программном обеспечении определяют исходя из последних полученных результатов и действий пользователя. Полученную таким образом информацию можно изучить, просматривая соответствующий фрагмент программы. В результате выдвигаются гипотезы об ошибках, которые затем проверяются. Если гипотеза верна, то детализируют информацию об ошибке, иначе — выдвигают другую гипотезу. Если в результате изучения данных никаких гипотез не появляется, то необходима дополнительная информация об ошибке.
Метод дедукции работает по следующему алгоритму. Сначала формируют множество причин, которые могли бы вызвать данное проявление ошибки. Затем, анализируя причины, исключают те, которые противоречат имеющимся данным. Если все причины исключены, то необходима дополнительная информация об ошибке и следует выполнить дополнительное тестирование исследуемого фрагмента. В противном случае наиболее вероятную гипотезу пытаются доказать. Если гипотеза объясняет полученные признаки ошибки, то ошибка найдена, иначе — проверяют следующую причину.
Метод обратного прослеживания используется для небольших программ и заключается в следующем. Определяется точка вывода неправильного результата. Затем строится гипотеза о значениях основных переменных, которые могли бы привести к получению этого результата. Исходя из этой гипотезы, делают предположения о значениях переменных в предыдущей точке. Процесс продолжают, пока не обнаружат причину ошибки.
Рассмотрим категории программных ошибок, которые встречаются наиболее часто.
Функциональные недостатки. Данные недостатки присущи программе, если она не делает того, что должна, выполняет одну из своих функций плохо или не полностью. Функции программы должны быть подробно описаны в ее спецификации, и именно на основе утвержденной спецификации тестировщик строит свою работу.
Недостатки пользовательского интерфейса. Лучше всего оценить удобство и правильность работы пользовательского интерфейса может только пользователь в процессе работы с ним. Проверить это возможно с помощью прототипа программного обеспечения, на котором проводятся обкатка и согласование всех требований к пользовательскому интерфейсу с дальнейшей фиксацией их в спецификации требований. После утверждения спецификации требований любые отклонения от нее или невыполнение последних являются ошибкой. Это в полной мере касается и пользовательского интерфейса.
Недостаточная производительность. При разработке некоторого программного продукта очень важной его характеристикой может оказаться скорость работы, иногда этот критерий задается в требованиях заказчика к программному обеспечению. Недопустимо, если программа не удовлетворяет заданным в спецификации требований характеристикам. Это уже ошибка, которая должна быть обязательно устранена.
Некорректная обработка ошибок. Правильно определив ошибку, программа должна выдать о ней сообщение. Отсутствие такого сообщения является ошибкой в работе программы.
Некорректная обработка граничных условий. Существует много различных граничных ситуаций. Любой аспект работы программы, к которому применимы понятия «больше» или «меньше», «раньше» или «позже», «первый» или «последний», «короче» или «длиннее», обязательно должен быть проверен на границах диапазона. Внутри диапазонов программа может работать правильно, а на их границах могут происходить неожиданные ситуации, которые, в свою очередь, приводят к ошибкам в работе программного обеспечения.
Ошибки вычислений. К ошибкам вычислений относятся ошибки, вызванные неправильным выбором алгоритма вычислений, неправильными формулами либо формулами, неприменимыми к обрабатываемым данным. Самыми распространенными среди ошибок вычислений являются ошибки округления.
Ошибки управления потоком. По логике работы программы вслед за первым действием должно быть выполнено второе. Если вместо этого выполняется третье или четвертое действие, значит, в управлении потоком допущена ошибка.
Ситуация гонок. Предположим, в системе ожидаются два события: А и Б. Если первым наступит событие А, то выполнение программы продолжится, а если событие Б, то в работе программы произойдет сбой. Разработчики предполагают, что первым всегда должно быть событие А, и не ожидают, что Б может выиграть гонки и наступить раньше. Такова классическая ситуация гонок. Тестировать ситуации гонок довольно сложно. Наиболее типичны они для систем, где параллельно выполняются взаимодействующие процессы и потоки, а также для многопользовательских систем реального времени. Ошибки в таких системах трудно воспроизвести, и на их выявление обычно требуется очень много времени.
Перегрузки. Сбои в работе программы могут происходить из-за нехватки памяти или отсутствия других необходимых системных ресурсов. У каждой программы свои пределы, программа может не справляться с повышенными нагрузками, например со слишком большими объемами данных. Вопрос в том, соответствуют ли реальные возможности программы, ее требования к ресурсам спецификации программы, и как она себя поведет при перегрузках.
Некорректная работа с аппаратурой компьютера. Программы могут отправлять аппаратным устройствам неверные данные, игнорировать их сообщения об ошибках, пытаться использовать устройства, которые заняты или вообще отсутствуют. Даже если нужное устройство просто неисправно, программа должна понять это, а не «зависать» при попытке к нему обратиться.
ФГБОУ ВПО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ. М Е. ЕВСЕВЬЕВА»
Физико – математический факультет
Кафедра информатики и вычислительной техники
КУРСОВАЯ РАБОТА
ПРОБЛЕМЫ КОДИРОВАНИЯ ИНФОРМАЦИИ
Автор курсовой работы___________________________________ Д.А. Храмов
Направление подготовки 050100.62 Педагогическое образование
Профиль Математика. Информатика.
Руководитель работы
д.ф.–м.н., проф. каф. ИВТ______________________________ Е.В. Щенникова
Саранск 2013
Содержание
Введение……………………………………………………………………………3
1 Кодирование информации………………………………………………………5
1.1 Кодирование текстовой информации…………………………………5
1.2 Кодирование графической информации……………………….……..6
1.3 Кодирование звуковой информации………………………………….9
2 Шум и защита от шума. Теория кодирования К.Шеннона …………………11
3 Способы обнаружения ошибок с их последующим исправлением…………13
4 Основные понятия корректирующих кодов…………………………………15
4.1 Линейные и групповые коды…………………………………………17
4.2 Код Хэмминга………………………………………………………….21
Заключение……………………………………………………………………… 27
Список литературы………………………………………………………………28
Введение
Кодирование – процесс представления информации в виде кода. Под термином «кодирование», как правило, понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Кодирование в узком смысле – способ сделать сообщение непонятным для всех, кто не владеет ключом кода.
Первым, кто использовал кодирование двух символьной информации, был Готфрид Вильгельм Лейбниц. Он считал: «Вычисление с помощью двоек … является для науки основным и порождает новые открытия. При сведении чисел к простым началам, каковыми являются 0 и 1, везде появляется чудесный порядок». Но, к сожалению, эта система была забыта.
Первым теоретическое решение проблемы передачи данных по зашумленным каналам предложил
Клод Шеннон, основоположник статистической теории информации. Работая в Bell Labs, Шеннон написал работу «Математическая теория передачи сообщений» (1948), где показал, что если пропускная способность канала выше энтропии источника сообщений, то сообщение можно закодировать так, что оно будет передано без излишних задержек.
Переход от теории к практике стал возможен благодаря усилиям Ричарда Хэмминга, коллеги Шеннона по Bell Labs, получившего известность за открытие класса кодов «коды Хэмминга».
Хэмминг первым предложил «коды с исправлением ошибок» (Error-Correcting Code, ECC). Современные модификации этих кодов используются во всех системах хранения данных и для обмена между процессором и оперативной памятью. Один из их вариантов, коды Рида-Соломона применяются в компакт-дисках, позволяя воспроизводить записи без скрипов и шумов, вызванных царапинами и пылинками. Существует множество версий кодов, построенных «по мотивам» Хэмминга, они различаются алгоритмами кодирования и количеством проверочных битов. Особое значение подобные коды приобрели в связи с развитием дальней космической связи с межпланетными станциями.
Цель моей курсовой работы, является ознакомление с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Эта проблема в настоящее время относится к числу наиболее актуальных проблем, т.к. при обработке, передачи и хранении информации мы стремимся к повышению ее надежности.
Объект: процесс кодирования информации.
Задачи:
-
Проанализировать пособия по теории информации и информационной безопасности.
-
Выявить формы представления кодирования информации.
-
Обнаружение ошибок (проблем).
-
Методы и способы исправления ошибок.
1 Кодирование информации
Современный ПК может обрабатывать различную информацию (числовую, текстовую, звуковую и видео). Вся информация в компьютере представлена в двоичном коде, т.е. Используется алфавит мощностью два. Это связанно, прежде всего, с тем, что удобно представлять в виде последовательности электрических импульсов (импульс отсутствует — 0, импульс есть — 1). Логическая последовательность нулей и единиц называется, машинным кодом.
1.1 Кодирование текстовой информации
В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.
Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту, т. е. I = 1 байт = 8 бит. При помощи формулы, которая связывает между собой количество возможных событий К и количество информации I, можно вычислить сколько различных символов можно закодировать (считая, что символы — это возможные события): К = 2I 28 = 256, т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов.
Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ — 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные, при помощи одной таблицы не будут правильно отображаться в другой кодировке.
В большинстве случаев о перекодировке текстовых документов заботится пользователь, а специальные программы — конвертеры, которые встроены в приложения.
Начиная с 1997г. последние версии Microsoft Windows Office поддерживают новую кодировку Unicode, которая на каждый символ отводит по 2 байта, а поэтому, можно закодировать не 256 символов, а 65536 различных символов.
1.2 Кодирование графической информации
В середине 50-х годов для больших ЭВМ, которые применялись в научных и военных исследованиях, впервые в графическом виде было реализовано представление данных. В настоящее время широко используются технологии обработки графической информации с помощью ПК.
Особенно интенсивно технология обработки графической информации с помощью компьютера стала развиваться в 80-х годах. Графическую информацию можно представлять в двух формах: аналоговой или дискретной. Живописное полотно, цвет которого изменяется непрерывно — это пример аналогового представления, а изображение, напечатанное при помощи струйного принтера и состоящее из отдельных точек разного цвета — это дискретное представление. Чем большее количество цветов используется (т. е. точка изображения может принимать больше возможных состояний), тем больше информации несет каждая точка, а, значит, увеличивается качество кодирования. Создание и хранение графических объектов возможно в нескольких видах — в виде векторного, фрактального или растрового изображения.
Отдельным предметом считается 3D (трехмерная) графика, в которой сочетаются векторный и растровый способы формирования изображений.
Если говорить о кодировании цветных графических изображений, то нужно рассмотреть принцип декомпозиции произвольного цвета на основные составляющие. Применяют несколько систем кодирования: HSB, RGB и CMYK.
1) Модель HSB характеризуется тремя компонентами: оттенок цвета (Hue), насыщенность цвета (Saturation) и яркость цвета (Brightness). Можно получить большое количество произвольных цветов, регулируя эти компоненты.
2) Принцип метода RGB заключается в следующем: известно, что любой цвет можно представить в виде комбинации трех цветов: красного (Red, R), зеленого (Green, G), синего (Blue, B). Другие цвета и их оттенки получаются за счет наличия или отсутствия этих составляющих.
3) Принцип метода CMYK. Эта цветовая модель используется при подготовке публикаций к печати. Каждому из основных цветов ставится в соответствие дополнительный цвет (дополняющий основной до белого).
Различают несколько режимов представления цветной графики:
1) полноцветный (TrueColor);
2) HighColor;
3) индексный.
При полноцветном режиме для кодирования яркости каждой из составляющих используют по 256 значений (восемь двоичных разрядов), то есть на кодирование цвета одного пикселя (в системе RGB) надо затратить 8*3=24 разряда. Это позволяет однозначно определять 16,5 млн цветов. Это довольно близко к чувствительности человеческого глаза. При кодировании с помощью системы CMYK для представления цветной графики надо иметь 8*4=32 двоичных разрядов.
Режим HighColor — это кодирование при помощи 16-разрядных двоичных чисел, то есть уменьшается количество двоичных разрядов при кодировании каждой точки. Но при этом значительно уменьшается диапазон кодируемых цветов.
При индексном кодировании цвета можно передать всего лишь 256 цветовых оттенков. Каждый цвет кодируется при помощи восьми бит данных. Но так как 256 значений не передают весь диапазон цветов, доступный человеческому глазу, то подразумевается, что к графическим данным прилагается палитра (справочная таблица), без которой воспроизведение будет неадекватным: море может получиться красным, а листья — синими. Сам код точки растра в данном случае означает не сам по себе цвет, а только его номер (индекс) в палитре. Отсюда и название режима — индексный.
Соответствие между количеством отображаемых цветов (К) и количеством бит для их кодировки (а) находиться по формуле: К = 2а («Таблица 1») .
«Таблица 1»
|
А |
К |
Достаточно для |
|
4 |
24 = 16 |
|
|
8 |
28 = 256 |
Рисованных изображений типа тех, что видим в мультфильмах, но недостаточно для изображений живой природы |
|
16 (HighColor) |
216 = 65536 |
Изображений, которые на картинках в журналах и на фотографиях |
|
24 (TrueColor) |
224 = 16 777 216 |
Обработки и передачи изображений, не уступающих по качеству наблюдаемым в живой природе |
1.3 Кодирование звуковой информации
С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, микрофон и колонки, может записывать, сохранять и воспроизводить звуковую информацию. Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда, тем он громче для человека, чем больше частота сигнала, тем выше тон. Программное обеспечение компьютера в настоящее время позволяет непрерывный звуковой сигнал преобразовывать в последовательность электрических импульсов, которые можно представить в двоичной форме.
Процесс преобразования звуковых волн в двоичный код в памяти компьютера:
Звуковая волна →Микрофон → Переменный электрический ток → Аудиоадаптер →Двоичный код → Память компьютера
Процесс воспроизведения звуковой информации, сохраненной в памяти компьютера:
Память компьютера → Двоичный код → Аудиоадаптер → Переменный электрический ток → Динамик → Звуковая волна
Аудиоадаптер (звуковая плата)– специальное устройство, подключаемое к компьютеру, предназначенное для преобразования электрических колебаний звуковой частоты в числовой двоичный код при вводе звука и для обратного преобразования (из числового кода в электрические колебания) при воспроизведении звука.
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины.
Затем полученный код из регистра переписывается в оперативную память компьютера.
Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Частота дискретизации – это количество измерений входного сигнала за 1 секунду.
Разрядность регистра– число бит в регистре аудиоадаптера.
2 Шум и защита от шума. Теория кодирования К.Шеннона
Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи возникают по техническим причинам: плохое качество линии связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Например, при беседе по телефону, мы слышим шум и треск. В таких случаях необходима защита от шума. Способы защиты бывают самыми разными. Использование экранированного кабеля вместо «голого» провода; применение различных фильтров, отделяющих полезный сигнал от шума и т.п.
Клодом Шенноном была разработана специальная теория кодирования, дающая методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования К. Шеннона как раз и позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи часто применяется следующий прием борьбы с потерей информации. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета, и если она не совпадает с первоначальной, то передача данного пакета повторяется. Так происходит пока исходная и конечная контрольные суммы не совпадут.
3 Способы обнаружения ошибок с их последующим исправлением
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
-
обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
-
обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
-
Исправление ошибок применяется на физическом уровне.
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникших при передаче информации под влиянием помех, а так же при её хранении.
При записи в данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении её используют для того, чтобы обнаружить или исправить ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
Коды обнаружения ошибок в отличии от кодов исправляющих ошибки, могут только установить факт наличия ошибки.
Фактически любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
4 Основные понятия корректирующих кодов
Среди корректирующих кодов широко используются циклические коды, в ЭВМ эти коды применяются при последовательной передаче данных между ЭВМ и внешними устройствами, а также при передаче данных по каналам связи. Для исправления двух и более ошибок (d0 5) используются циклические коды БЧХ (Боуза — Чоудхури — Хоквингема), а также Рида-Соломона, которые широко используются в устройствах цифровой записи звука на магнитную ленту или оптические компакт-диски и позволяющие осуществлять коррекцию групповых ошибок. Способность кода обнаруживать и исправлять ошибки достигается за счет введений избыточности в кодовые комбинации, т.е. кодовым комбинациям из к двоичных информационных символов, поступающих на вход кодирующего устройства, соответствует на выходе последовательность из n двоичных символов (такой код называется (n, k) — кодом).
Если N0 = 2n-общее число кодовых комбинаций, а N = 2k — число разрешенных, то число запрещенных кодовых комбинаций равно
N0-N = 2n -2k.
При этом число ошибок, которое приводит к запрещенной кодовой комбинации равно (1).
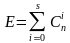
где S — кратность ошибки, т.е. количество искаженных символов в кодовой комбинации S = 0, 1, 2, …
Cni— сочетания из n элементов по i, вычисляемое, по формуле (2)
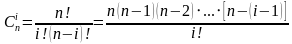
для S = 0; 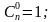
S = 1; 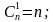
S = 2; 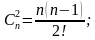
S= 3; 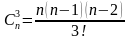
Для исправления S ошибок количество комбинаций кодового слова, составленного из m проверочных разрядов N = 2m, должно быть больше возможного числа ошибок (3), при этом количество обнаруживаемых ошибок в два раза больше, чем исправляемых
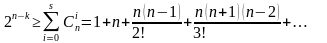
2m
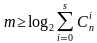
Для одиночной ошибки, как наиболее вероятной 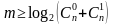
В зависимости от исходных данных кода (n или k) можно использовать
формулы (4).
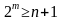
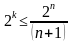
При этом, m = [log2(1+n)] или m = [log2 {(k+1)+ [log2(k+1)]}], где квадратные скобки обозначают округление до большего целого.
В таблице приведены соотношения между длиной кодовой комбинации и количеством информационных и контрольных разрядов для кода исправляющего одиночную ошибку, а также эффективность использования канала связи.
Для исправления двукратной ошибки (5).
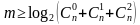
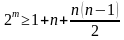
Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи.
Например, для кода (31, 26) скорость передачи информации равна
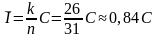
«Таблица 2»
|
n |
7 |
10 |
15 |
31 |
63 |
127 |
255 |
|
k |
4 |
6 |
11 |
26 |
57 |
120 |
247 |
|
m |
3 |
4 |
4 |
5 |
6 |
7 |
8 |
|
|
0,57 |
0,6 |
0,75 |
0,84 |
0,9 |
0,95 |
0,97 |
Как видно из таблицы , чем больше n, тем эффективнее используется канал.
4.1 Линейные и групповые коды
Линейным называется код, в котором проверочные символы представляют собой линейные комбинации информационных.
Групповым называется код, который образует алгебраическую группу по отношению операции сложения по модулю два.
Свойство линейного кода: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий этому коду.
Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами равно минимальному весу ненулевых векторов. Вес кодового вектора равен числу единиц в кодовой комбинации.
Групповые коды удобно задавать при помощи матриц, размерность которых определяется параметрами k и n. Число строк равно k, а число столбцов равно n = k+m.(6).
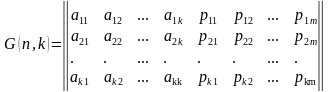
Коды, порождаемые этими матрицами, называются (n, k)-кодами, а соответствующие им матрицы порождающими (образующими, производящими). Порождающая матрица G состоит из информационной Ikk и проверочной Rkm матриц. Она является сжатым описанием линейного кода и может быть представлена в канонической (типовой) форме (7).
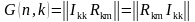
В качестве информационной матрицы удобно использовать единичную матрицу, ранг которой определяется количеством информационных разрядов (8).

Строки единичной матрицы представляют собой линейно-независимые комбинации (базисные вектора), т.е. их по парное суммирование по модулю два не приводит к нулевой строке.
Строки порождающей матрицы представляют собой первые k комбинаций корректирующего кода, а остальные кодовые комбинации могут быть получены в результате суммирования по модулю два всевозможных сочетаний этих строк.
Столбцы добавочной матрицы Rkm определяют правила формирования проверок. Число единиц в каждой строке добавочной матрицы должно удовлетворять условию r1 d0-1, но число единиц определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, и чем их больше, тем сложнее аппаратура.
Производящая матрица кода G(7,4) может иметь вид

Процесс кодирования состоит во взаимно — однозначном соответствии к-разрядных информационных слов — I и n-разрядных кодовых слов – с(9)
c=IG (9)
Например: информационному слову I=[1 0 1 0] соответствует кодовое слово (10).

При этом, информационная часть остается без изменений, а корректирующие разряды определяются путем суммирования по модулю два тех строк проверочной матрицы, номера которых совпадают с номерами разрядов, содержащих единицу в информационной части кода.
Процесс декодирования состоит в определении соответствия принятого кодового слова, переданному информационному. Это осуществляется с помощью проверочной матрицы H(n, k) (11).
где RmkT -транспонированная проверочная матрица (поменять строки на столбцы); Imm— единичная матрица.
Для (7, 4)- кода проверочная матрица имеет вид (12).
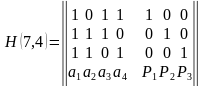
Между G(n ,k) и H(n, k) существует однозначная связь, т.к. они определяются в соответствии с правилами проверки, при этом для любого кодового слова должно выполняться равенство cHT= 0.
Строки проверочной матрицы определяют правила формирования проверок. Для (7, 4)-кода соответствует (13).
p1+a1+a2a4 = S1 ;
p2+a1+a2a3 = S2 ; (13)
p3+a1+a3a4 = S3 .
Полученный синдром сравниваем со столбцами матрицы и определяем разряд, в котором произошла ошибка, номер столбца равен номеру ошибочного разряда. Для исправления ошибки ошибочный бит необходимо проинвертировать.
4.2 Код Хемминга
Код Хэмминга относится к классу линейных кодов и представляет собой систематический код – код, в котором информационные и контрольные биты, расположены на строго определенных местах в кодовой комбинации.
Код Хэмминга, как и любой (n, k)- код, содержит к информационных и m = n-k избыточных (проверочных) бит.
Избыточная часть кода строится т.о. чтобы можно было при декодировании не только установить наличие ошибки но, и указать номер позиции, в которой произошла ошибка, а значит, и исправить ее, инвертировав значение соответствующего бита.
Существуют различные методы реализации кода Хэмминга и кодов которые являются модификацией кода Хэмминга. Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
-
По заданному количеству информационных символов — k, либо информационных комбинаций N = 2k , используя соотношения (14).
n = k+m, 2n (n+1)2k и 2m n+1 (14)
m = [log2 {(k+1)+ [log2(k+1)]}]
вычисляют основные параметры кода n и m.
2. Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону 2i,где i=1, 2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1 ) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно m = n-k. В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение — 0, в противном случае — 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n –чисел разрядностью – m или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до (2k –1) перечисленных в возрастающем порядке. Для m = 3 проверочная матрица имеет вид (15).
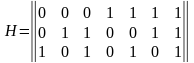
Количество разрядов m — определяет количество проверок («Таблица 3»).
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1, b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку — коэффициенты которые содержат 1 в третьем разряде и т.д.
«Таблица 3»
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) -разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.
В ЭВМ код Хэмминга чаще всего используется для обнаружения и исправления ошибок в ОП, памяти с обнаружением и исправлением ошибок ECCMemory (ErrorCheckingandCorrecting). Код Хэмминга используется как при параллельной, так и при последовательной записи. В ЭВМ значительная часть интенсивности потока ошибок приходится на ОП. Причинами постоянных неисправностей являются отказы ИС, а случайных изменение содержимого ОП за счет флуктуации питающего напряжения, кратковременных помех и излучений. Неисправность может быть в одном бите, линии выборки разряда, слова либо всей ИС. Сбой может возникнуть при формировании кода (параллельного), адреса или данных, поэтому защищать необходимо и то и др. Обычно дешифратор адреса встроен в микро схему и недоступен для потребителя. Наиболее часто ошибки дают ячейки памяти ЗУ, поэтому главным образом защищают записываемые и считываемые данные.
Наибольшее применение в ЗУ нашли коды Хэмминга с dmin=4, исправляющие одиночные ошибки и обнаруживающие двойные.
Проверочные символы записываются либо в основное, либо специальное ЗУ. Для каждого записываемого информационного слова (а не байта, как при контроле по паритету) по определенным правилам вычисляется функция свертки, результат которой разрядностью в несколько бит также записывается в память. Для 16-ти разрядного информационного слова используется 6 дополнительных бит (32 — 7 бит, 64 – 8 бит). При считывании информации схема контроля («Рис. 1»), используя избыточные биты, позволяет обнаружить ошибки различной кратности или исправить одиночную ошибку. Возможны различные варианты поведения системы:
-
автоматическое исправление ошибки без уведомления системы;
-
исправление однократной ошибки и уведомление системы только о многократных ошибках;
-
не исправление ошибки, а только уведомление системы об ошибках;
Модуль памяти со встроенной схемой исправления ошибок – EOS 72/64 (ECConSimm). Аналог микросхема к 555 вж 1 -это 16 разрядная схема с обнаружением и исправлением ошибок (ОИО) по коду Хэмминга G(22, 16), использование которой позволяет исправить однократные ошибки и обнаружить все двух кратные ошибки в ЗУ.
Избыточные (контрольные) разряды позволяют обнаружить и исправить ошибки в ЗУ в процессе записи и хранения информации.
В составе ВЖ-1 используются 16 информационных и 6 контрольных разрядов. (DB — информационное слово, CB — контрольное слово).
При записи осуществляется формирование кода, состоящего из 16 информационных и 6 контрольных разрядов, представляющих результат суммирование по модулю 2 восьми информационных разрядов в соответствии с кодом Хэмминга. Сформированные контрольные разряды вместе с информационными поступают на схему и записываются в ЗУ.

«Рис. 1» — схема контроля
При считывании шестнадцатиразрядное слово декодируется, восстанавливаясь вместе с 6 разрядным словом контрольным, поступают на схему сравнения и контроля. Если достигнуто равенство всех контрольных разрядов и двоичных слов, то ошибки нет.
Любая однократная ошибка в 16 разрядном слове данных изменяет 3 байта в 6 разрядном контрольном слове. Обнаруженный ошибочный бит инвертируется.
Заключение
Цель моей работы достигнута: я познакомился с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Рассмотрел циклические коды, исправляющие более 2 ошибок (к ним относятся коды БЧХ (Боуза — Чоудхури — Хоквингема) и Рида-Соломона) и линейные коды (коды Хемминга). Все они основываются на избыточности информации.
Научились находить эту избыточность с помощью формул. Узнал, что любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
Познакомился с различными способами кодирования различных видов информации: текстовой, графической и звуковой.
Список литературы
-
Недвоичные арифметические корректирующие коды, проблемы передачи информации / В.М. Гриценко — 4-е изд. – 1969. – 19 – 27 с.
-
Помехоустойчивые коды в системах связи / Б.М. Золотник — M.: Радио и связь, 1989.—232 c.
-
Информационная безопасность. Лабораторный практикум: учебное пособие / А.В. Бабаш, Е.К. Баранова, Ю.Н. Мельникова. — М.: КНОРУС, 2012. – 136 с.
-
Теория передачи сигналов / Кловский Д.Д. — M.: Cвязь, 1984.
-
Цифровое кодирование звуковых сигналов / Ковалгин Ю.A., Вологдин Э.И. — Изд-во Kорона-принт, 2004. – 240с.
-
Курс теории информации / Колесников B.Д., Полтырев Г.Ш. — M.: Наука, 1982. 416 с.
-
Микропроцессорные кодеры и декодеры / В.М. Муттер, Г.A. Петров и др.—M.: Радио и связь, 1991.—184 с.
-
Экономное кодирование дискретной информации / Семенюк В. В. – СПб: СПбГИТМО (ТУ), 2001. – 115 с.